Sampling Lights Directly
The problem with sampling uniformly over all directions is that lights are no more likely to be sampled than any arbirary or unimportant direction. We could use shadow rays to solve for the direct lighting at any given point. Instead, I’ll just use a PDF that sends more rays to the light. We can then turn around and change that PDF to send more rays in whatever direction we want.
It’s really easy to pick a random direction toward the light; just pick a random point on the light and send a ray in that direction. But we'll need to know the PDF, $p(\omega)$, so that we're not biasing our render. But what is that?
Getting the PDF of a Light
For a light with a surface area of $A$, if we sample uniformly on that light, the PDF on the surface is just $\frac{1}{A}$. How much area does the entire surface of the light take up if its projected back onto the unit sphere? Fortunately, there is a simple correspondence, as outlined in this diagram:
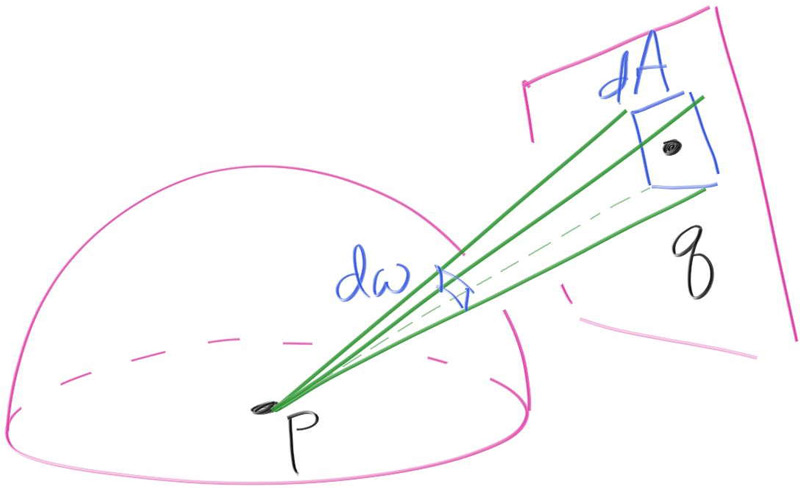
If we look at a small area $dA$ on the light, the probability of sampling it is $\operatorname{p_q}(q) \cdot dA$. On the sphere, the probability of sampling the small area $d\omega$ on the sphere is $\operatorname{p}(\omega) \cdot d\omega$. There is a geometric relationship between $d\omega$ and $dA$:
$$ d\omega = \frac{dA \cdot \cos(\theta)}{\operatorname{distance}^2(p,q)} $$
Since the probability of sampling $d\omega$ and $dA$ must be the same, then
$$ \operatorname{p}(\omega) \cdot d\omega = \operatorname{p_q}(q) \cdot dA $$
$$ \operatorname{p}(\omega)
\cdot \frac{dA \cdot \cos(\theta)}{\operatorname{distance}^2(p,q)}
= \operatorname{p_q}(q) \cdot dA $$
We know that if we sample uniformly on the light the PDF on the surface is $\frac{1}{A}$:
$$ \operatorname{p_q}(q) = \frac{1}{A} $$
$$ \operatorname{p}(\omega) \cdot \frac{dA \cdot \cos(\theta)}{\operatorname{distance}^2(p,q)}
= \frac{dA}{A} $$
So
$$ \operatorname{p}(\omega) = \frac{\operatorname{distance}^2(p,q)}{\cos(\theta) \cdot A} $$
Light Sampling
We can hack our ray_color() function to sample the light in a very hard-coded fashion just to
check that we got the math and concept right:
class camera {
...
private:
color ray_color(const ray& r, int depth, const hittable& world) const {
hit_record rec;
// If we've exceeded the ray bounce limit, no more light is gathered.
if (depth <= 0)
return color(0,0,0);
// If the ray hits nothing, return the background color.
if (!world.hit(r, interval(0.001, infinity), rec))
return background;
ray scattered;
color attenuation;
double pdf;
color color_from_emission = rec.mat->emitted(rec.u, rec.v, rec.p);
if (!rec.mat->scatter(r, rec, attenuation, scattered, pdf))
return color_from_emission;
auto on_light = point3(random_double(213,343), 554, random_double(227,332));
auto to_light = on_light - rec.p;
auto distance_squared = to_light.length_squared();
to_light = unit_vector(to_light);
if (dot(to_light, rec.normal) < 0)
return color_from_emission;
double light_area = (343-213)*(332-227);
auto light_cosine = fabs(to_light.y());
if (light_cosine < 0.000001)
return color_from_emission;
pdf = distance_squared / (light_cosine * light_area);
scattered = ray(rec.p, to_light, r.time());
double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);
color color_from_scatter =
(attenuation * scattering_pdf * ray_color(scattered, depth-1, world)) / pdf;
return color_from_emission + color_from_scatter;
}
};
With 10 samples per pixel this yields:

This is about what we would expect from something that samples only the light sources, so this appears to work.
Switching to Unidirectional Light
The noisy pops around the light on the ceiling are because the light is two-sided and there is a small space between light and ceiling. We probably want to have the light just emit down. We can do that by letting the emitted member function of hittable take extra information:
class material {
public:
...
virtual color emitted(
const ray& r_in, const hit_record& rec, double u, double v, const point3& p
) const {
return color(0,0,0);
}
...
};
class diffuse_light : public material {
public:
...
color emitted(const ray& r_in, const hit_record& rec, double u, double v, const point3& p)
const override {
if (!rec.front_face)
return color(0,0,0);
return emit->value(u, v, p);
}
...
};
This gives us:
