Generating Random Directions
In this and the next two chapters, we'll harden our understanding and our tools.
Random Directions Relative to the Z Axis
Let’s first figure out how to generate random directions. We already have a method to generate random directions using the rejection method, so let's create one using the inversion method. To simplify things, assume the $z$ axis is the surface normal, and $\theta$ is the angle from the normal. We'll set everything up in terms of the $z$ axis this chapter. Next chapter we’ll get them oriented to the surface normal vector. We will only deal with distributions that are rotationally symmetric about $z$. So $p(\omega) = f(\theta)$.
Given a directional PDF on the sphere (where $p(\omega) = f(\theta)$), the one dimensional PDFs on $\theta$ and $\phi$ are:
$$ a(\phi) = \frac{1}{2\pi} $$
$$ b(\theta) = 2\pi f(\theta)\sin(\theta) $$
For uniform random numbers $r_1$ and $r_2$, we solve for the CDF of $\theta$ and $\phi$ so that we can invert the CDF to derive the random number generator.
$$ r_1 = \int_{0}^{\phi} a(\phi') d\phi' $$
$$ = \int_{0}^{\phi} \frac{1}{2\pi} d\phi' $$
$$ = \frac{\phi}{2\pi} $$
Invert to solve for $\phi$:
$$ \phi = 2 \pi \cdot r_1 $$
This should match with your intuition. To solve for a random $\phi$ you can take a uniform random number in the interval [0,1] and multiply by $2\pi$ to cover the full range of all possible $\phi$ values, which is just [0,$2\pi$]. You may not have a fully formed intuition for how to solve for a random value of $\theta$, so let's walk through the math to help you get set up. We rewrite $\phi$ as $\phi'$ and $\theta$ as $\theta'$ just like before, as a formality. For $\theta$ we have:
$$ r_2 = \int_{0}^{\theta} b(\theta') d\theta' $$
$$ = \int_{0}^{\theta} 2 \pi f(\theta') \sin(\theta') d\theta' $$
Let’s try some different functions for $f()$. Let’s first try a uniform density on the sphere. The area of the unit sphere is $4\pi$, so a uniform $p(\omega) = \frac{1}{4\pi}$ on the unit sphere.
$$ r_2 = \int_{0}^{\theta} 2 \pi \frac{1}{4\pi} \sin(\theta') d\theta' $$
$$ = \int_{0}^{\theta} \frac{1}{2} \sin(\theta') d\theta' $$
$$ = \frac{-\cos(\theta)}{2} - \frac{-\cos(0)}{2} $$
$$ = \frac{1 - \cos(\theta)}{2} $$
Solving for $\cos(\theta)$ gives:
$$ \cos(\theta) = 1 - 2 r_2 $$
We don’t solve for theta because we probably only need to know $\cos(\theta)$ anyway, and don’t want needless $\arccos()$ calls running around.
To generate a unit vector direction toward $(\theta,\phi)$ we convert to Cartesian coordinates:
$$ x = \cos(\phi) \cdot \sin(\theta) $$
$$ y = \sin(\phi) \cdot \sin(\theta) $$
$$ z = \cos(\theta) $$
And using the identity $\cos^2 + \sin^2 = 1$, we get the following in terms of random $(r_1,r_2)$:
$$ x = \cos(2\pi \cdot r_1)\sqrt{1 - (1-2 r_2)^2} $$
$$ y = \sin(2\pi \cdot r_1)\sqrt{1 - (1-2 r_2)^2} $$
$$ z = 1 - 2 r_2 $$
Simplifying a little, $(1 - 2 r_2)^2 = 1 - 4r_2 + 4r_2^2$, so:
$$ x = \cos(2 \pi r_1) \cdot 2 \sqrt{r_2(1 - r_2)} $$
$$ y = \sin(2 \pi r_1) \cdot 2 \sqrt{r_2(1 - r_2)} $$
$$ z = 1 - 2 r_2 $$
We can output some of these:
#include "rtweekend.h"
#include <iostream>
#include <math.h>
int main() {
for (int i = 0; i < 200; i++) {
auto r1 = random_double();
auto r2 = random_double();
auto x = cos(2*pi*r1)*2*sqrt(r2*(1-r2));
auto y = sin(2*pi*r1)*2*sqrt(r2*(1-r2));
auto z = 1 - 2*r2;
std::cout << x << " " << y << " " << z << '\n';
}
}
And plot them for free on plot.ly (a great site with 3D scatterplot support):
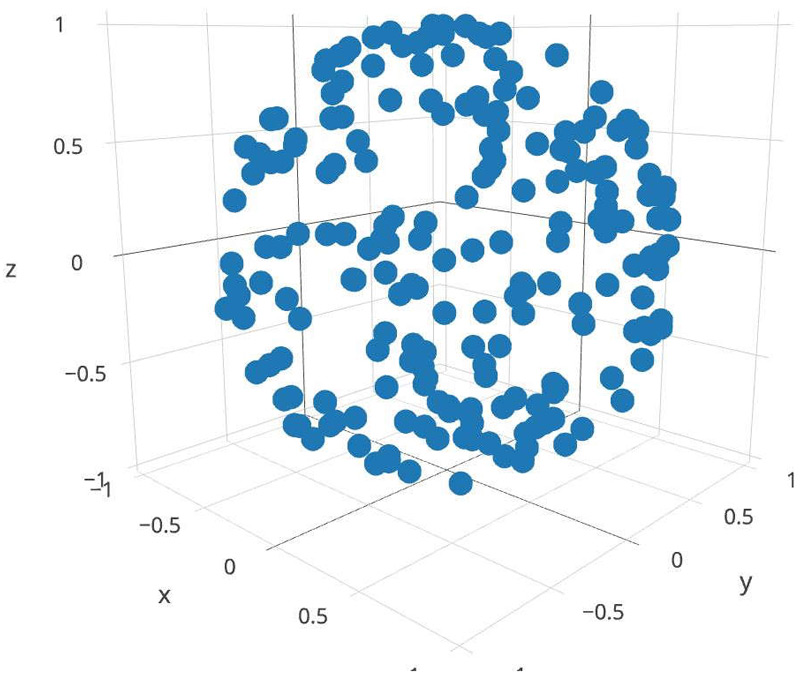
On the plot.ly website you can rotate that around and see that it appears uniform.
Uniform Sampling a Hemisphere
Now let’s derive uniform on the hemisphere. The density being uniform on the hemisphere means $p(\omega) = f(\theta) = \frac{1}{2\pi}$. Just changing the constant in the theta equations yields:
$$ r_2 = \int_{0}^{\theta} b(\theta') d\theta' $$
$$ = \int_{0}^{\theta} 2 \pi f(\theta') \sin(\theta') d\theta' $$
$$ = \int_{0}^{\theta} 2 \pi \frac{1}{2\pi} \sin(\theta') d\theta' $$
$$ \ldots $$
$$ \cos(\theta) = 1 - r_2 $$
This means that $\cos(\theta)$ will vary from 1 to 0, so $\theta$ will vary from 0 to $\pi/2$, which means that nothing will go below the horizon. Rather than plot it, we'll solve for a 2D integral with a known solution. Let’s integrate cosine cubed over the hemisphere (just picking something arbitrary with a known solution). First we'll solve the integral by hand:
$$ \int_\omega \cos^3(\theta) dA $$
$$ = \int_{0}^{2 \pi} \int_{0}^{\pi /2} \cos^3(\theta) \sin(\theta) d\theta d\phi $$
$$ = 2 \pi \int_{0}^{\pi/2} \cos^3(\theta) \sin(\theta) d\theta = \frac{\pi}{2} $$
Now for integration with importance sampling. $p(\omega) = \frac{1}{2\pi}$, so we average $f()/p() = \cos^3(\theta) / \frac{1}{2\pi}$, and we can test this:
#include "rtweekend.h"
#include <iostream>
#include <iomanip>
#include <math.h>
double f(double r1, double r2) {
// auto x = cos(2*pi*r1)*2*sqrt(r2*(1-r2));
// auto y = sin(2*pi*r1)*2*sqrt(r2*(1-r2));
auto z = 1 - r2;
double cos_theta = z;
return cos_theta*cos_theta*cos_theta;
}
double pdf(double r1, double r2) {
return 1.0 / (2.0*pi);
}
int main() {
int N = 1000000;
auto sum = 0.0;
for (int i = 0; i < N; i++) {
auto r1 = random_double();
auto r2 = random_double();
sum += f(r1, r2) / pdf(r1, r2);
}
std::cout << std::fixed << std::setprecision(12);
std::cout << "PI/2 = " << pi / 2.0 << '\n';
std::cout << "Estimate = " << sum / N << '\n';
}
Cosine Sampling a Hemisphere
We'll now continue trying to solve for cosine cubed over the horizon, but we'll change our PDF to generate directions with $p(\omega) = f(\theta) = \cos(\theta) / \pi$.
$$ r_2 = \int_{0}^{\theta} b(\theta') d\theta' $$
$$ = \int_{0}^{\theta} 2 \pi f(\theta') \sin(\theta') d\theta' $$
$$ = \int_{0}^{\theta} 2 \pi \frac{\cos(\theta')}{\pi} \sin(\theta') d\theta' $$
$$ = 1 - \cos^2(\theta) $$
So,
$$ \cos(\theta) = \sqrt{1 - r_2} $$
We can save a little algebra on specific cases by noting
$$ z = \cos(\theta) = \sqrt{1 - r_2} $$
$$ x = \cos(\phi) \sin(\theta) = \cos(2 \pi r_1) \sqrt{1 - z^2} = \cos(2 \pi r_1) \sqrt{r_2} $$
$$ y = \sin(\phi) \sin(\theta) = \sin(2 \pi r_1) \sqrt{1 - z^2} = \sin(2 \pi r_1) \sqrt{r_2} $$
Here's a function that generates random vectors weighted by this PDF:
inline vec3 random_cosine_direction() {
auto r1 = random_double();
auto r2 = random_double();
auto phi = 2*pi*r1;
auto x = cos(phi)*sqrt(r2);
auto y = sin(phi)*sqrt(r2);
auto z = sqrt(1-r2);
return vec3(x, y, z);
}
#include "rtweekend.h"
#include <iostream>
#include <iomanip>
#include <math.h>
double f(const vec3& d) {
auto cos_theta = d.z();
return cos_theta*cos_theta*cos_theta;
}
double pdf(const vec3& d) {
return d.z() / pi;
}
int main() {
int N = 1000000;
auto sum = 0.0;
for (int i = 0; i < N; i++) {
vec3 d = random_cosine_direction();
sum += f(d) / pdf(d);
}
std::cout << std::fixed << std::setprecision(12);
std::cout << "PI/2 = " << pi / 2.0 << '\n';
std::cout << "Estimate = " << sum / N << '\n';
}
We can generate other densities later as we need them. This random_cosine_direction() function
produces a random direction weighted by $\cos(\theta)$ where $\theta$ is the angle from the $z$
axis.