Cleaning Up PDF Management
So far I have the ray_color() function create two hard-coded PDFs:
p0()related to the shape of the lightp1()related to the normal vector and type of surface
We can pass information about the light (or whatever hittable we want to sample) into the
ray_color() function, and we can ask the material function for a PDF (we would have to add
instrumentation to do that). We also need to know if the scattered ray is specular, and we can do
this either by asking the hit() function or the material class.
Diffuse Versus Specular
One thing we would like to allow for is a material -- like varnished wood -- that is partially ideal
specular (the polish) and partially diffuse (the wood). Some renderers have the material generate
two rays: one specular and one diffuse. I am not fond of branching, so I would rather have the
material randomly decide whether it is diffuse or specular. The catch with that approach is that we
need to be careful when we ask for the PDF value, and ray_color() needs to be aware of whether
this ray is diffuse or specular. Fortunately, we have decided that we should only call the
pdf_value() if it is diffuse, so we can handle that implicitly.
We can redesign material and stuff all the new arguments into a class like we did for hittable:
class scatter_record {
public:
color attenuation;
shared_ptr<pdf> pdf_ptr;
bool skip_pdf;
ray skip_pdf_ray;
};
class material {
public:
...
virtual bool scatter(
const ray& r_in, const hit_record& rec, scatter_record& srec
) const {
return false;
}
...
};
The lambertian material becomes simpler:
class lambertian : public material {
public:
lambertian(const color& a) : albedo(make_shared<solid_color>(a)) {}
lambertian(shared_ptr<texture> a) : albedo(a) {}
bool scatter(const ray& r_in, const hit_record& rec, scatter_record& srec) const override {
srec.attenuation = albedo->value(rec.u, rec.v, rec.p);
srec.pdf_ptr = make_shared<cosine_pdf>(rec.normal);
srec.skip_pdf = false;
return true;
}
double scattering_pdf(const ray& r_in, const hit_record& rec, const ray& scattered) const {
auto cosine = dot(rec.normal, unit_vector(scattered.direction()));
return cosine < 0 ? 0 : cosine/pi;
}
private:
shared_ptr<texture> albedo;
};
As does the isotropic material:
class isotropic : public material {
public:
isotropic(color c) : albedo(make_shared<solid_color>(c)) {}
isotropic(shared_ptr<texture> a) : albedo(a) {}
bool scatter(const ray& r_in, const hit_record& rec, scatter_record& srec) const override {
srec.attenuation = albedo->value(rec.u, rec.v, rec.p);
srec.pdf_ptr = make_shared<sphere_pdf>();
srec.skip_pdf = false;
return true;
}
double scattering_pdf(const ray& r_in, const hit_record& rec, const ray& scattered)
const override {
return 1 / (4 * pi);
}
private:
shared_ptr<texture> albedo;
};
And ray_color() changes are small:
class camera {
...
private:
...
color ray_color(const ray& r, int depth, const hittable& world, const hittable& lights)
const {
hit_record rec;
// If we've exceeded the ray bounce limit, no more light is gathered.
if (depth <= 0)
return color(0,0,0);
// If the ray hits nothing, return the background color.
if (!world.hit(r, interval(0.001, infinity), rec))
return background;
scatter_record srec;
color color_from_emission = rec.mat->emitted(r, rec, rec.u, rec.v, rec.p);
if (!rec.mat->scatter(r, rec, srec))
return color_from_emission;
auto light_ptr = make_shared<hittable_pdf>(lights, rec.p);
mixture_pdf p(light_ptr, srec.pdf_ptr);
ray scattered = ray(rec.p, p.generate(), r.time());
auto pdf_val = p.value(scattered.direction());
double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);
color sample_color = ray_color(scattered, depth-1, world, lights);
color color_from_scatter = (srec.attenuation * scattering_pdf * sample_color) / pdf_val;
return color_from_emission + color_from_scatter;
}
};
Handling Specular
We have not yet dealt with specular surfaces, nor instances that mess with the surface normal. But
this design is clean overall, and those are all fixable. For now, I will just fix specular. Metal
and dielectric materials are easy to fix.
class metal : public material {
public:
metal(const color& a, double f) : albedo(a), fuzz(f < 1 ? f : 1) {}
bool scatter(const ray& r_in, const hit_record& rec, scatter_record& srec) const override {
srec.attenuation = albedo;
srec.pdf_ptr = nullptr;
srec.skip_pdf = true;
vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
srec.skip_pdf_ray =
ray(rec.p, reflected + fuzz*random_in_unit_sphere(), r_in.time());
return true;
}
private:
color albedo;
double fuzz;
};
...
class dielectric : public material {
public:
dielectric(double index_of_refraction) : ir(index_of_refraction) {}
bool scatter(const ray& r_in, const hit_record& rec, scatter_record& srec) const override {
srec.attenuation = color(1.0, 1.0, 1.0);
srec.pdf_ptr = nullptr;
srec.skip_pdf = true;
double refraction_ratio = rec.front_face ? (1.0/ir) : ir;
vec3 unit_direction = unit_vector(r_in.direction());
double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
bool cannot_refract = refraction_ratio * sin_theta > 1.0;
vec3 direction;
if (cannot_refract || reflectance(cos_theta, refraction_ratio) > random_double())
direction = reflect(unit_direction, rec.normal);
else
direction = refract(unit_direction, rec.normal, refraction_ratio);
srec.skip_pdf_ray = ray(rec.p, direction, r_in.time());
return true;
}
...
};
Note that if the fuzziness is nonzero, this surface isn’t really ideally specular, but the implicit sampling works just like it did before. We're effectively skipping all of our PDF work for the materials that we're treating specularly.
ray_color() just needs a new case to generate an implicitly sampled ray:
class camera {
...
private:
...
color ray_color(const ray& r, int depth, const hittable& world, const hittable& lights)
const {
...
if (!rec.mat->scatter(r, rec, srec))
return color_from_emission;
if (srec.skip_pdf) {
return srec.attenuation * ray_color(srec.skip_pdf_ray, depth-1, world, lights);
}
auto light_ptr = make_shared<hittable_pdf>(lights, rec.p);
mixture_pdf p(light_ptr, srec.pdf_ptr);
...
}
};
We'll check our work by changing a block to metal. We'd also like to swap out one of the blocks for a glass object, but we'll push that off for the next section. Glass objects are difficult to render well, so we'd like to make a PDF for them, but we have some more work to do before we're able to do that.
int main() {
...
// Light
world.add(make_shared<quad>(point3(213,554,227), vec3(130,0,0), vec3(0,0,105), light));
// Box 1
shared_ptr<material> aluminum = make_shared<metal>(color(0.8, 0.85, 0.88), 0.0);
shared_ptr<hittable> box1 = box(point3(0,0,0), point3(165,330,165), aluminum);
box1 = make_shared<rotate_y>(box1, 15);
box1 = make_shared<translate>(box1, vec3(265,0,295));
world.add(box1);
// Box 2
shared_ptr<hittable> box2 = box(point3(0,0,0), point3(165,165,165), white);
box2 = make_shared<rotate_y>(box2, -18);
box2 = make_shared<translate>(box2, vec3(130,0,65));
world.add(box2);
// Light Sources
hittable_list lights;
auto m = shared_ptr<material>();
lights.add(make_shared<quad>(point3(343,554,332), vec3(-130,0,0), vec3(0,0,-105), m));
...
}
The resulting image has a noisy reflection on the ceiling because the directions toward the box are not sampled with more density.

Sampling a Sphere Object
The noisiness on the ceiling could be reduced by making a PDF of the metal block. We would also want
a PDF for the block if we made it glass. But making a PDF for a block is quite a bit of work and
isn't terribly interesting, so let’s create a PDF for a glass sphere instead. It's quicker and makes
for a more interesting render. We need to figure out how to sample a sphere to determine an
appropriate PDF distribution. If we want to sample a sphere from a point outside of the sphere, we
can't just pick a random point on its surface and be done. If we did that, we would frequently pick
a point on the far side of the sphere, which would be occluded by the front side of the sphere. We
need a way to uniformly sample the side of the sphere that is visible from an arbitrary point. When
we sample a sphere’s solid angle uniformly from a point outside the sphere, we are really just
sampling a cone uniformly. The cone axis goes from the ray origin through the sphere center, with
the sides of the cone tangent to the sphere -- see illustration below. Let’s say the code has
theta_max. Recall from the Generating Random Directions chapter that to sample $\theta$ we have:
$$ r_2 = \int_{0}^{\theta} 2 \pi f(\theta') \sin(\theta') d\theta' $$
Here $f(\theta')$ is an as-of-yet uncalculated constant $C$, so:
$$ r_2 = \int_{0}^{\theta} 2 \pi C \sin(\theta') d\theta' $$
If we solve through the calculus:
$$ r_2 = 2\pi \cdot C \cdot (1-\cos(\theta)) $$
So
$$ cos(\theta) = 1 - \frac{r_2}{2 \pi \cdot C} $$
We are constraining our distribution so that the random direction must be less than $\theta_{max}$. This means that the integral from 0 to $\theta_{max}$ must be one, and therefore $r_2 = 1$. We can use this to solve for $C$:
$$ r_2 = 2\pi \cdot C \cdot (1-\cos(\theta)) $$ $$ 1 = 2\pi \cdot C \cdot (1-\cos(\theta_{max})) $$ $$ C = \frac{1}{2\pi \cdot (1-\cos(\theta_{max})} $$
Which gives us an equality between $\theta$, $\theta_{max}$, and $r_2$:
$$ \cos(\theta) = 1 + r_2 \cdot (\cos(\theta_{max})-1) $$
We sample $\phi$ like before, so:
$$ z = \cos(\theta) = 1 + r_2 \cdot (\cos(\theta_{max}) - 1) $$ $$ x = \cos(\phi) \cdot \sin(\theta) = \cos(2\pi \cdot r_1) \cdot \sqrt{1-z^2} $$ $$ y = \sin(\phi) \cdot \sin(\theta) = \sin(2\pi \cdot r_1) \cdot \sqrt{1-z^2} $$
Now what is $\theta_{max}$?
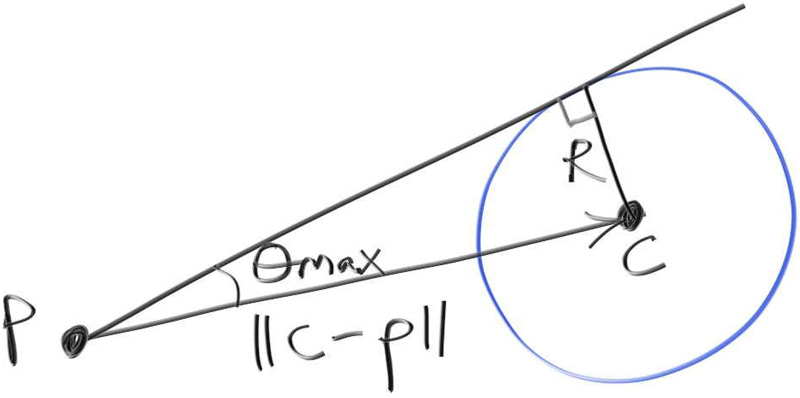
We can see from the figure that $\sin(\theta_{max}) = R / length(\mathbf{c} - \mathbf{p})$. So:
$$ \cos(\theta_{max}) = \sqrt{1 - \frac{R^2}{length^2(\mathbf{c} - \mathbf{p})}} $$
We also need to evaluate the PDF of directions. For a uniform distribution toward the sphere the PDF is $1/\mathit{solid_angle}$. What is the solid angle of the sphere? It has something to do with the $C$ above. It is -- by definition -- the area on the unit sphere, so the integral is
$$ \mathit{solid angle} = \int_{0}^{2\pi} \int_{0}^{\theta_{max}} \sin(\theta) = 2 \pi \cdot (1-\cos(\theta_{max})) $$
It’s good to check the math on all such calculations. I usually plug in the extreme cases (thank you for that concept, Mr. Horton -- my high school physics teacher). For a zero radius sphere $\cos(\theta_{max}) = 0$, and that works. For a sphere tangent at $\mathbf{p}$, $\cos(\theta_{max}) = 0$, and $2\pi$ is the area of a hemisphere, so that works too.
Updating the Sphere Code
The sphere class needs the two PDF-related functions:
class sphere : public hittable {
public:
...
double pdf_value(const point3& o, const vec3& v) const override {
// This method only works for stationary spheres.
hit_record rec;
if (!this->hit(ray(o, v), interval(0.001, infinity), rec))
return 0;
auto cos_theta_max = sqrt(1 - radius*radius/(center1 - o).length_squared());
auto solid_angle = 2*pi*(1-cos_theta_max);
return 1 / solid_angle;
}
vec3 random(const point3& o) const override {
vec3 direction = center1 - o;
auto distance_squared = direction.length_squared();
onb uvw;
uvw.build_from_w(direction);
return uvw.local(random_to_sphere(radius, distance_squared));
}
private:
...
static vec3 random_to_sphere(double radius, double distance_squared) {
auto r1 = random_double();
auto r2 = random_double();
auto z = 1 + r2*(sqrt(1-radius*radius/distance_squared) - 1);
auto phi = 2*pi*r1;
auto x = cos(phi)*sqrt(1-z*z);
auto y = sin(phi)*sqrt(1-z*z);
return vec3(x, y, z);
}
};
We can first try just sampling the sphere rather than the light:
int main() {
...
// Light
world.add(make_shared<quad>(point3(213,554,227), vec3(130,0,0), vec3(0,0,105), light));
// Box
shared_ptr<hittable> box1 = box(point3(0,0,0), point3(165,330,165), white);
box1 = make_shared<rotate_y>(box1, 15);
box1 = make_shared<translate>(box1, vec3(265,0,295));
world.add(box1);
// Glass Sphere
auto glass = make_shared<dielectric>(1.5);
world.add(make_shared<sphere>(point3(190,90,190), 90, glass));
// Light Sources
hittable_list lights;
auto m = shared_ptr<material>();
lights.add(make_shared<quad>(point3(343,554,332), vec3(-130,0,0), vec3(0,0,-105), m));
...
}
This yields a noisy room, but the caustic under the sphere is good. It took five times as long as sampling the light did for my code. This is probably because those rays that hit the glass are expensive!

Adding PDF Functions to Hittable Lists
We should probably just sample both the sphere and the light. We can do that by creating a mixture
density of their two distributions. We could do that in the ray_color() function by passing a list
of hittables in and building a mixture PDF, or we could add PDF functions to hittable_list. I
think both tactics would work fine, but I will go with instrumenting hittable_list.
class hittable_list : public hittable {
public:
...
double pdf_value(const point3& o, const vec3& v) const override {
auto weight = 1.0/objects.size();
auto sum = 0.0;
for (const auto& object : objects)
sum += weight * object->pdf_value(o, v);
return sum;
}
vec3 random(const vec3& o) const override {
auto int_size = static_cast<int>(objects.size());
return objects[random_int(0, int_size-1)]->random(o);
}
...
};
We assemble a list to pass to render() from main():
int main() {
...
// Light Sources
hittable_list lights;
auto m = shared_ptr<material>();
lights.add(make_shared<quad>(point3(343,554,332), vec3(-130,0,0), vec3(0,0,-105), m));
lights.add(make_shared<sphere>(point3(190, 90, 190), 90, m));
...
}
And we get a decent image with 1000 samples as before:

Handling Surface Acne
An astute reader pointed out there are some black specks in the image above. All Monte Carlo Ray Tracers have this as a main loop:
If you find yourself getting some form of acne in your renders, and this acne is white or black --
where one "bad" sample seems to kill the whole pixel -- then that sample is probably a huge number
or a NaN (Not A Number). This particular acne is probably a NaN. Mine seems to come up once in
every 10–100 million rays or so.
So big decision: sweep this bug under the rug and check for NaNs, or just kill NaNs and hope
this doesn't come back to bite us later. I will always opt for the lazy strategy, especially when I
know that working with floating point is hard. First, how do we check for a NaN? The one thing I
always remember for NaNs is that a NaN does not equal itself. Using this trick, we update the
write_color() function to replace any NaN components with zero:
void write_color(std::ostream &out, color pixel_color, int samples_per_pixel) {
auto r = pixel_color.x();
auto g = pixel_color.y();
auto b = pixel_color.z();
// Replace NaN components with zero.
if (r != r) r = 0.0;
if (g != g) g = 0.0;
if (b != b) b = 0.0;
// Divide the color by the number of samples and gamma-correct for gamma=2.0.
auto scale = 1.0 / samples_per_pixel;
r = sqrt(scale * r);
g = sqrt(scale * g);
b = sqrt(scale * b);
// Write the translated [0,255] value of each color component.
static const interval intensity(0.000, 0.999);
out << static_cast<int>(256 * intensity.clamp(r)) << ' '
<< static_cast<int>(256 * intensity.clamp(g)) << ' '
<< static_cast<int>(256 * intensity.clamp(b)) << '\n';
}
Happily, the black specks are gone:
