Rays, a Simple Camera, and Background
The ray Class
The one thing that all ray tracers have is a ray class and a computation of what color is seen along
a ray. Let’s think of a ray as a function $\mathbf{P}(t) = \mathbf{A} + t \mathbf{b}$. Here
$\mathbf{P}$ is a 3D position along a line in 3D. $\mathbf{A}$ is the ray origin and $\mathbf{b}$ is
the ray direction. The ray parameter $t$ is a real number (double in the code). Plug in a
different $t$ and $\mathbf{P}(t)$ moves the point along the ray. Add in negative $t$ values and you
can go anywhere on the 3D line. For positive $t$, you get only the parts in front of $\mathbf{A}$,
and this is what is often called a half-line or a ray.
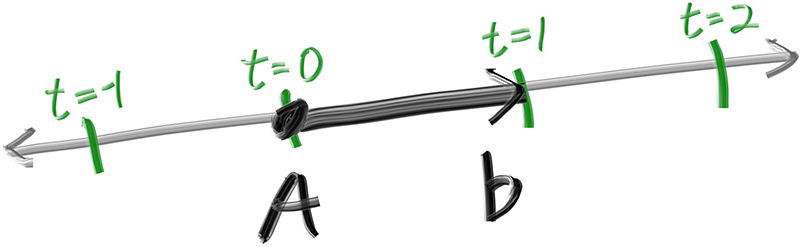
We can represent the idea of a ray as a class, and represent the function $\mathbf{P}(t)$ as a
function that we'll call ray::at(t):
#ifndef RAY_H
#define RAY_H
#include "vec3.h"
class ray {
public:
ray() {}
ray(const point3& origin, const vec3& direction) : orig(origin), dir(direction) {}
point3 origin() const { return orig; }
vec3 direction() const { return dir; }
point3 at(double t) const {
return orig + t*dir;
}
private:
point3 orig;
vec3 dir;
};
#endif
Sending Rays Into the Scene
Now we are ready to turn the corner and make a ray tracer. At its core, a ray tracer sends rays through pixels and computes the color seen in the direction of those rays. The involved steps are
1. Calculate the ray from the “eye” through the pixel,
2. Determine which objects the ray intersects, and
3. Compute a color for the closest intersection point.
When first developing a ray tracer, I always do a simple camera for getting the code up and running.
I’ve often gotten into trouble using square images for debugging because I transpose $x$ and $y$ too often, so we’ll use a non-square image. A square image has a 1∶1 aspect ratio, because its width is the same as its height. Since we want a non-square image, we'll choose 16∶9 because it's so common. A 16∶9 aspect ratio means that the ratio of image width to image height is 16∶9. Put another way, given an image with a 16∶9 aspect ratio,
$$\text{width} / \text{height} = 16 / 9 = 1.7778$$
For a practical example, an image 800 pixels wide by 400 pixels high has a 2∶1 aspect ratio.
The image's aspect ratio can be determined from the ratio of its height to its width. However, since we have a given aspect ratio in mind, it's easier to set the image's width and the aspect ratio, and then using this to calculate for its height. This way, we can scale up or down the image by changing the image width, and it won't throw off our desired aspect ratio. We do have to make sure that when we solve for the image height the resulting height is at least 1.
In addition to setting up the pixel dimensions for the rendered image, we also need to set up a virtual viewport through which to pass our scene rays. The viewport is a virtual rectangle in the 3D world that contains the grid of image pixel locations. If pixels are spaced the same distance horizontally as they are vertically, the viewport that bounds them will have the same aspect ratio as the rendered image. The distance between two adjacent pixels is called the pixel spacing, and square pixels is the standard.
To start things off, we'll choose an arbitrary viewport height of 2.0, and scale the viewport width to give us the desired aspect ratio. Here's a snippet of what this code will look like:
auto aspect_ratio = 16.0 / 9.0;
int image_width = 400;
// Calculate the image height, and ensure that it's at least 1.
int image_height = static_cast<int>(image_width / aspect_ratio);
image_height = (image_height < 1) ? 1 : image_height;
// Viewport widths less than one are ok since they are real valued.
auto viewport_height = 2.0;
auto viewport_width = viewport_height * (static_cast<double>(image_width)/image_height);
If you're wondering why we don't just use aspect_ratio when computing viewport_width, it's
because the value set to aspect_ratio is the ideal ratio, it may not be the actual ratio
between image_width and image_height. If image_height was allowed to be real valued--rather
than just an integer--then it would fine to use aspect_ratio. But the actual ratio
between image_width and image_height can vary based on two parts of the code. First,
integer_height is rounded down to the nearest integer, which can increase the ratio. Second, we
don't allow integer_height to be less than one, which can also change the actual aspect ratio.
Note that aspect_ratio is an ideal ratio, which we approximate as best as possible with the
integer-based ratio of image width over image height.
In order for our viewport proportions to exactly match our image proportions, we use the calculated
image aspect ratio to determine our final viewport width.
Next we will define the camera center: a point in 3D space from which all scene rays will originate (this is also commonly referred to as the eye point). The vector from the camera center to the viewport center will be orthogonal to the viewport. We'll initially set the distance between the viewport and the camera center point to be one unit. This distance is often referred to as the focal length.
For simplicity we'll start with the camera center at $(0,0,0)$. We'll also have the y-axis go up, the x-axis to the right, and the negative z-axis pointing in the viewing direction. (This is commonly referred to as right-handed coordinates.)
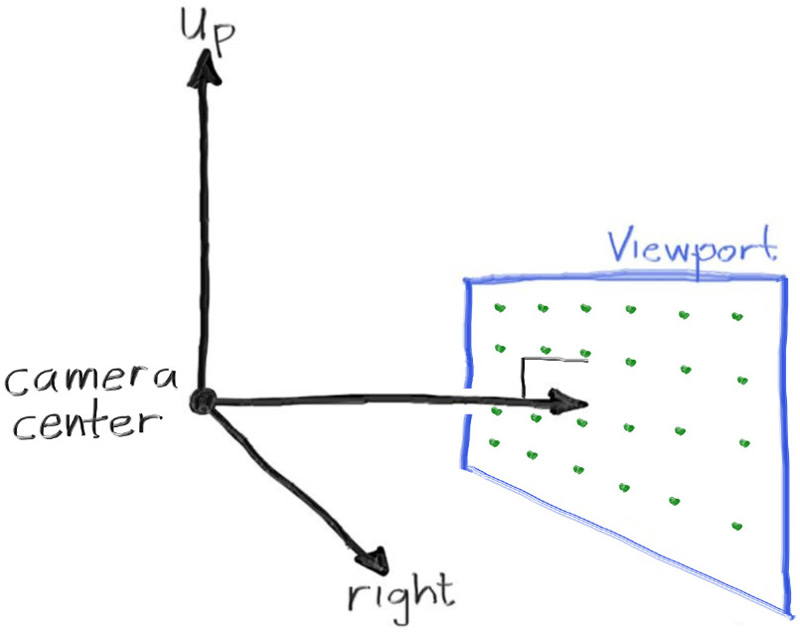
Now the inevitable tricky part. While our 3D space has the conventions above, this conflicts with our image coordinates, where we want to have the zeroth pixel in the top-left and work our way down to the last pixel at the bottom right. This means that our image coordinate Y-axis is inverted: Y increases going down the image.
As we scan our image, we will start at the upper left pixel (pixel $0,0$), scan left-to-right across each row, and then scan row-by-row, top-to-bottom. To help navigate the pixel grid, we'll use a vector from the left edge to the right edge ($\mathbf{V_u}$), and a vector from the upper edge to the lower edge ($\mathbf{V_v}$).
Our pixel grid will be inset from the viewport edges by half the pixel-to-pixel distance. This way, our viewport area is evenly divided into width × height identical regions. Here's what our viewport and pixel grid look like:
![]()
In this figure, we have the viewport, the pixel grid for a 7×5 resolution image, the viewport
upper left corner $\mathbf{Q}$, the pixel $\mathbf{P_{0,0}}$ location, the viewport vector
$\mathbf{V_u}$ (viewport_u), the viewport vector $\mathbf{V_v}$ (viewport_v), and the pixel
delta vectors $\mathbf{\Delta u}$ and $\mathbf{\Delta v}$.
Drawing from all of this, here's the code that implements the camera.
We'll stub in a function ray_color(const ray& r) that returns the color for a given scene ray
-- which we'll set to always return black for now.
#include "color.h"
#include "ray.h"
#include "vec3.h"
#include <iostream>
color ray_color(const ray& r) {
return color(0,0,0);
}
int main() {
// Image
auto aspect_ratio = 16.0 / 9.0;
int image_width = 400;
// Calculate the image height, and ensure that it's at least 1.
int image_height = static_cast<int>(image_width / aspect_ratio);
image_height = (image_height < 1) ? 1 : image_height;
// Camera
auto focal_length = 1.0;
auto viewport_height = 2.0;
auto viewport_width = viewport_height * (static_cast<double>(image_width)/image_height);
auto camera_center = point3(0, 0, 0);
// Calculate the vectors across the horizontal and down the vertical viewport edges.
auto viewport_u = vec3(viewport_width, 0, 0);
auto viewport_v = vec3(0, -viewport_height, 0);
// Calculate the horizontal and vertical delta vectors from pixel to pixel.
auto pixel_delta_u = viewport_u / image_width;
auto pixel_delta_v = viewport_v / image_height;
// Calculate the location of the upper left pixel.
auto viewport_upper_left = camera_center
- vec3(0, 0, focal_length) - viewport_u/2 - viewport_v/2;
auto pixel00_loc = viewport_upper_left + 0.5 * (pixel_delta_u + pixel_delta_v);
// Render
std::cout << "P3\n" << image_width << " " << image_height << "\n255\n";
for (int j = 0; j < image_height; ++j) {
std::clog << "\rScanlines remaining: " << (image_height - j) << ' ' << std::flush;
for (int i = 0; i < image_width; ++i) {
auto pixel_center = pixel00_loc + (i * pixel_delta_u) + (j * pixel_delta_v);
auto ray_direction = pixel_center - camera_center;
ray r(camera_center, ray_direction);
color pixel_color = ray_color(r);
write_color(std::cout, pixel_color);
}
}
std::clog << "\rDone. \n";
}
Notice that in the code above, I didn't make ray_direction a unit vector, because I think not
doing that makes for simpler and slightly faster code.
Now we'll fill in the ray_color(ray) function to implement a simple gradient.
This function will linearly blend white and blue depending on the height of the $y$ coordinate
after scaling the ray direction to unit length (so $-1.0 < y < 1.0$).
Because we're looking at the $y$ height after normalizing the vector, you'll notice a horizontal
gradient to the color in addition to the vertical gradient.
I'll use a standard graphics trick to linearly scale $0.0 ≤ a ≤ 1.0$. When $a = 1.0$, I want blue. When $a = 0.0$, I want white. In between, I want a blend. This forms a “linear blend”, or “linear interpolation”. This is commonly referred to as a lerp between two values. A lerp is always of the form
$$ \mathit{blendedValue} = (1-a)\cdot\mathit{startValue} + a\cdot\mathit{endValue}, $$
with $a$ going from zero to one.
#include "color.h"
#include "ray.h"
#include "vec3.h"
#include <iostream>
color ray_color(const ray& r) {
vec3 unit_direction = unit_vector(r.direction());
auto a = 0.5*(unit_direction.y() + 1.0);
return (1.0-a)*color(1.0, 1.0, 1.0) + a*color(0.5, 0.7, 1.0);
}
In our case this produces:
