Positionable Camera
Cameras, like dielectrics, are a pain to debug, so I always develop mine incrementally. First, let’s allow for an adjustable field of view (fov). This is the visual angle from edge to edge of the rendered image. Since our image is not square, the fov is different horizontally and vertically. I always use vertical fov. I also usually specify it in degrees and change to radians inside a constructor -- a matter of personal taste.
Camera Viewing Geometry
First, we'll keep the rays coming from the origin and heading to the $z = -1$ plane. We could make it the $z = -2$ plane, or whatever, as long as we made $h$ a ratio to that distance. Here is our setup:
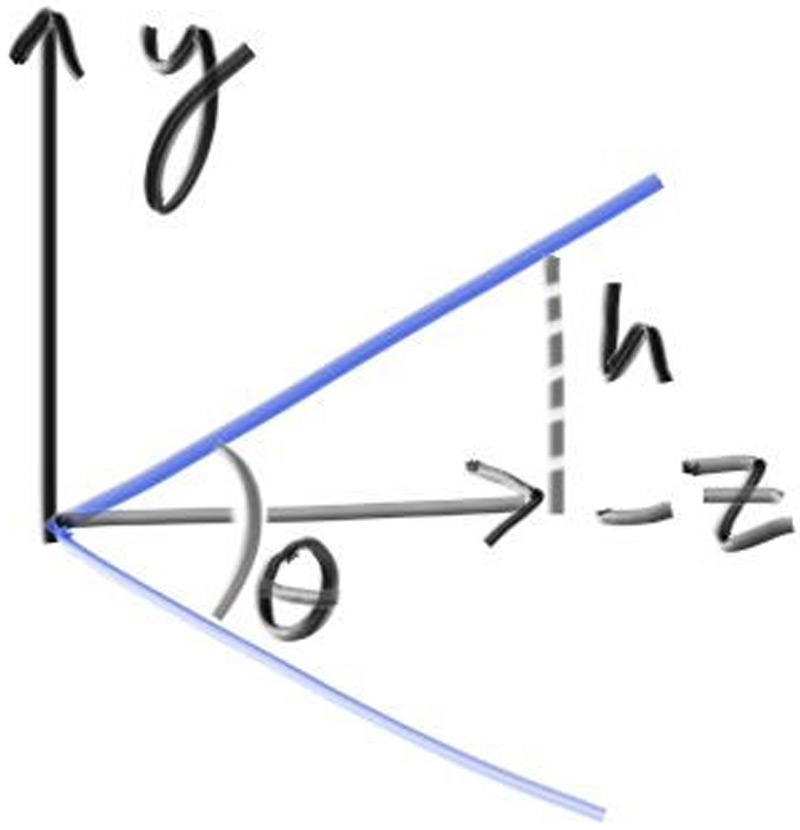
This implies $h = \tan(\frac{\theta}{2})$. Our camera now becomes:
class camera {
public:
double aspect_ratio = 1.0; // Ratio of image width over height
int image_width = 100; // Rendered image width in pixel count
int samples_per_pixel = 10; // Count of random samples for each pixel
int max_depth = 10; // Maximum number of ray bounces into scene
double vfov = 90; // Vertical view angle (field of view)
void render(const hittable& world) {
...
private:
...
void initialize() {
image_height = static_cast<int>(image_width / aspect_ratio);
image_height = (image_height < 1) ? 1 : image_height;
center = point3(0, 0, 0);
// Determine viewport dimensions.
auto focal_length = 1.0;
auto theta = degrees_to_radians(vfov);
auto h = tan(theta/2);
auto viewport_height = 2 * h * focal_length;
auto viewport_width = viewport_height * (static_cast<double>(image_width)/image_height);
// Calculate the vectors across the horizontal and down the vertical viewport edges.
auto viewport_u = vec3(viewport_width, 0, 0);
auto viewport_v = vec3(0, -viewport_height, 0);
// Calculate the horizontal and vertical delta vectors from pixel to pixel.
pixel_delta_u = viewport_u / image_width;
pixel_delta_v = viewport_v / image_height;
// Calculate the location of the upper left pixel.
auto viewport_upper_left =
center - vec3(0, 0, focal_length) - viewport_u/2 - viewport_v/2;
pixel00_loc = viewport_upper_left + 0.5 * (pixel_delta_u + pixel_delta_v);
}
...
};
We'll test out these changes with a simple scene of two touching spheres, using a 90° field of view.
int main() {
hittable_list world;
auto R = cos(pi/4);
auto material_left = make_shared<lambertian>(color(0,0,1));
auto material_right = make_shared<lambertian>(color(1,0,0));
world.add(make_shared<sphere>(point3(-R, 0, -1), R, material_left));
world.add(make_shared<sphere>(point3( R, 0, -1), R, material_right));
camera cam;
cam.aspect_ratio = 16.0 / 9.0;
cam.image_width = 400;
cam.samples_per_pixel = 100;
cam.max_depth = 50;
cam.vfov = 90;
cam.render(world);
}
This gives us the rendering:

Positioning and Orienting the Camera
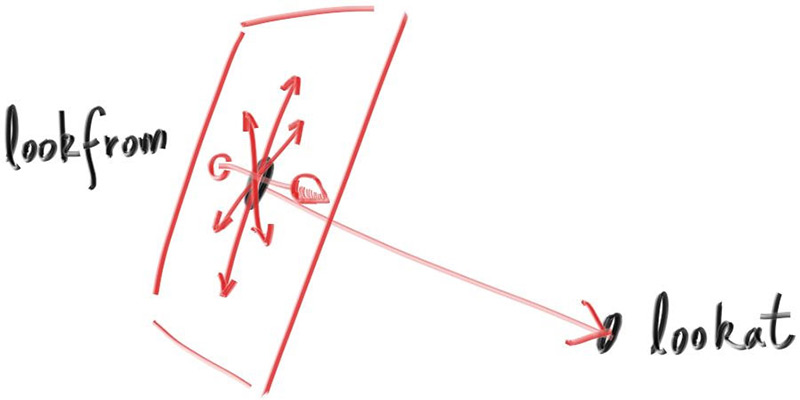
To get an arbitrary viewpoint, let’s first name the points we care about. We’ll call the position where we place the camera lookfrom, and the point we look at lookat. (Later, if you want, you could define a direction to look in instead of a point to look at.)
We also need a way to specify the roll, or sideways tilt, of the camera: the rotation around the
lookat-lookfrom axis.
Another way to think about it is that even if you keep lookfrom and lookat constant, you can
still rotate your head around your nose. What we need is a way to specify an “up” vector for the
camera.
We can specify any up vector we want, as long as it's not parallel to the view direction. Project this up vector onto the plane orthogonal to the view direction to get a camera-relative up vector. I use the common convention of naming this the “view up” (vup) vector. After a few cross products and vector normalizations, we now have a complete orthonormal basis $(u,v,w)$ to describe our camera’s orientation. $u$ will be the unit vector pointing to camera right, $v$ is the unit vector pointing to camera up, $w$ is the unit vector pointing opposite the view direction (since we use right-hand coordinates), and the camera center is at the origin.
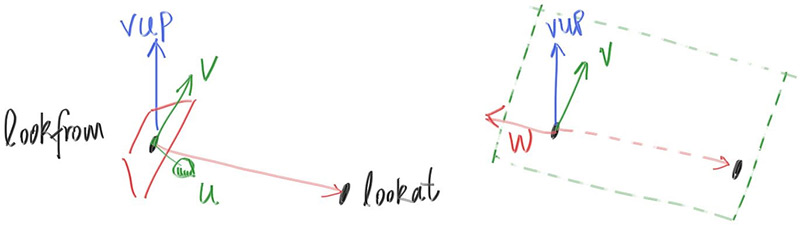
Like before, when our fixed camera faced $-Z$, our arbitrary view camera faces $-w$. Keep in mind that we can -- but we don’t have to -- use world up $(0,1,0)$ to specify vup. This is convenient and will naturally keep your camera horizontally level until you decide to experiment with crazy camera angles.
class camera {
public:
double aspect_ratio = 1.0; // Ratio of image width over height
int image_width = 100; // Rendered image width in pixel count
int samples_per_pixel = 10; // Count of random samples for each pixel
int max_depth = 10; // Maximum number of ray bounces into scene
double vfov = 90; // Vertical view angle (field of view)
point3 lookfrom = point3(0,0,-1); // Point camera is looking from
point3 lookat = point3(0,0,0); // Point camera is looking at
vec3 vup = vec3(0,1,0); // Camera-relative "up" direction
...
private:
int image_height; // Rendered image height
point3 center; // Camera center
point3 pixel00_loc; // Location of pixel 0, 0
vec3 pixel_delta_u; // Offset to pixel to the right
vec3 pixel_delta_v; // Offset to pixel below
vec3 u, v, w; // Camera frame basis vectors
void initialize() {
image_height = static_cast<int>(image_width / aspect_ratio);
image_height = (image_height < 1) ? 1 : image_height;
center = lookfrom;
// Determine viewport dimensions.
auto focal_length = (lookfrom - lookat).length();
auto theta = degrees_to_radians(vfov);
auto h = tan(theta/2);
auto viewport_height = 2 * h * focal_length;
auto viewport_width = viewport_height * (static_cast<double>(image_width)/image_height);
// Calculate the u,v,w unit basis vectors for the camera coordinate frame.
w = unit_vector(lookfrom - lookat);
u = unit_vector(cross(vup, w));
v = cross(w, u);
// Calculate the vectors across the horizontal and down the vertical viewport edges.
vec3 viewport_u = viewport_width * u; // Vector across viewport horizontal edge
vec3 viewport_v = viewport_height * -v; // Vector down viewport vertical edge
// Calculate the horizontal and vertical delta vectors from pixel to pixel.
pixel_delta_u = viewport_u / image_width;
pixel_delta_v = viewport_v / image_height;
// Calculate the location of the upper left pixel.
auto viewport_upper_left = center - (focal_length * w) - viewport_u/2 - viewport_v/2;
pixel00_loc = viewport_upper_left + 0.5 * (pixel_delta_u + pixel_delta_v);
}
...
private:
};
We'll change back to the prior scene, and use the new viewpoint:
int main() {
hittable_list world;
auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_center = make_shared<lambertian>(color(0.1, 0.2, 0.5));
auto material_left = make_shared<dielectric>(1.5);
auto material_right = make_shared<metal>(color(0.8, 0.6, 0.2), 0.0);
world.add(make_shared<sphere>(point3( 0.0, -100.5, -1.0), 100.0, material_ground));
world.add(make_shared<sphere>(point3( 0.0, 0.0, -1.0), 0.5, material_center));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), 0.5, material_left));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), -0.4, material_left));
world.add(make_shared<sphere>(point3( 1.0, 0.0, -1.0), 0.5, material_right));
camera cam;
cam.aspect_ratio = 16.0 / 9.0;
cam.image_width = 400;
cam.samples_per_pixel = 100;
cam.max_depth = 50;
cam.vfov = 90;
cam.lookfrom = point3(-2,2,1);
cam.lookat = point3(0,0,-1);
cam.vup = vec3(0,1,0);
cam.render(world);
}
to get:

And we can change field of view:
to get:
